Wir lieben Daten – und einer der schönsten Erscheinungsformen der Datenwelt bringt wohl jedes Unternehmen mit sich: die Zeitreihe. Heute wollen wir am Beispiel von Unternehmensinsolvenzen eine kleine Einführung in Zeitreihenanalysen geben. Wie so häufig im Bereich Data Science, richtet sich auch dieser Artikel an die Leser, die sich ein wenig einlesen wollen.
Zeitreihen
Der Grundgedanke ist denkbar einfach: Bei der Zeireihe handelt es sich um Ereignisse, die in mehr oder weniger regelmäßigen Abständen, nacheinander und daher über die Zeit auftreten. Was gibt es da also im Unternehmen? So ziemlich alles: Umsätze, Aufwände, Produktionskennzahlen…einfach alles was über die Zeit und wiederholend anfällt.
Das spannende an Zeitreihen ist, dass sie meist sehr viel mehr Information beinhalten, als man auf den ersten Blick denkt. Dinge wie Trends, Saisonalitäten und natürlich die Prognose interessieren dabei. Grund Genug der Zeitreihenanalyse mal ein wenig auf den Grund zu gehen. Ziel für heute ist es grob abzuschätzen, was man recht schnell und einfach machen kann, um ein Gefühl für eine Zeitreihe zu bekommen. Wir wollen keine technischen Fähigkeiten vermitteln, sondern einfach mal zeigen, wie man vorgehen kann.
Natürlich nehmen wir uns wieder öffentlich verfügbare Daten vor. Diesmal geht es um Insolvenzen. Die Daten sind recht nett, denn einerseits liegen sie halbwegs kontinuierlich vor und anderseits kann man an ihnen gut zeigen, wann Forecast-Modelle Schwierigkeiten mit sich bringen.
Ein Gefühl für die Daten entwickeln
Das statistische Bundesamt liefert uns monatliche Daten zu den eröffneten Insolvenzverfahren für Unternehmen seit Januar 2003. Bis zum Januar 2017 sieht das für Deutschland übrigens so aus:
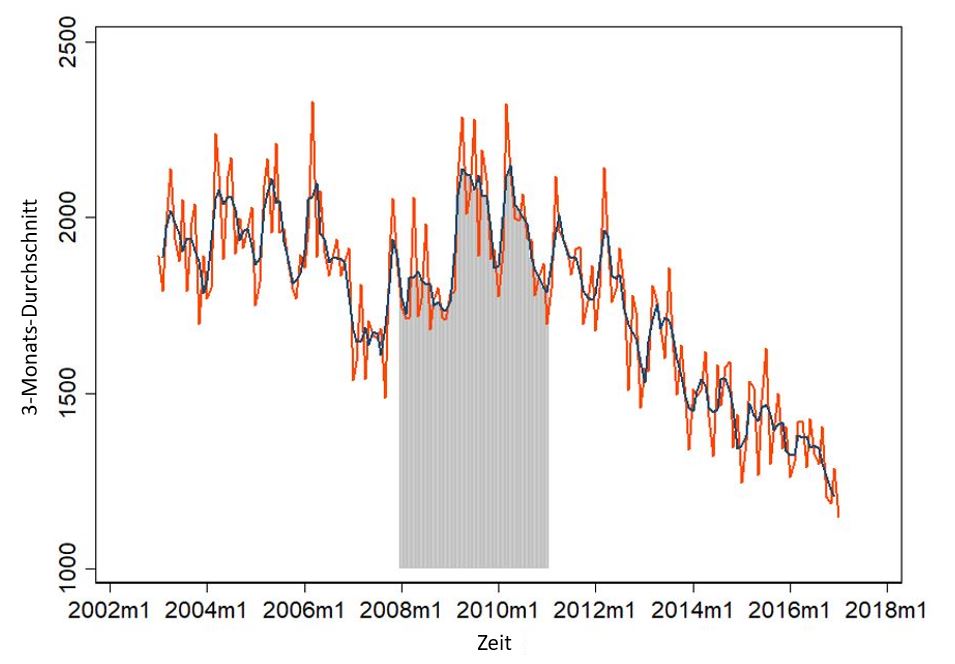
Die in der Mitte liegende Linie ist der 3-Monats-Durchschnitt. Aber was sagt uns dieser kleine Graph? In Summe irgendwie zwischen so 1200 und 2300 Insolvenzanträge. Es zeigt sich aber noch mehr. Vielleicht ist das einfacher zu sehen, wenn wir uns ein einzelne Jahre rausnehmen:
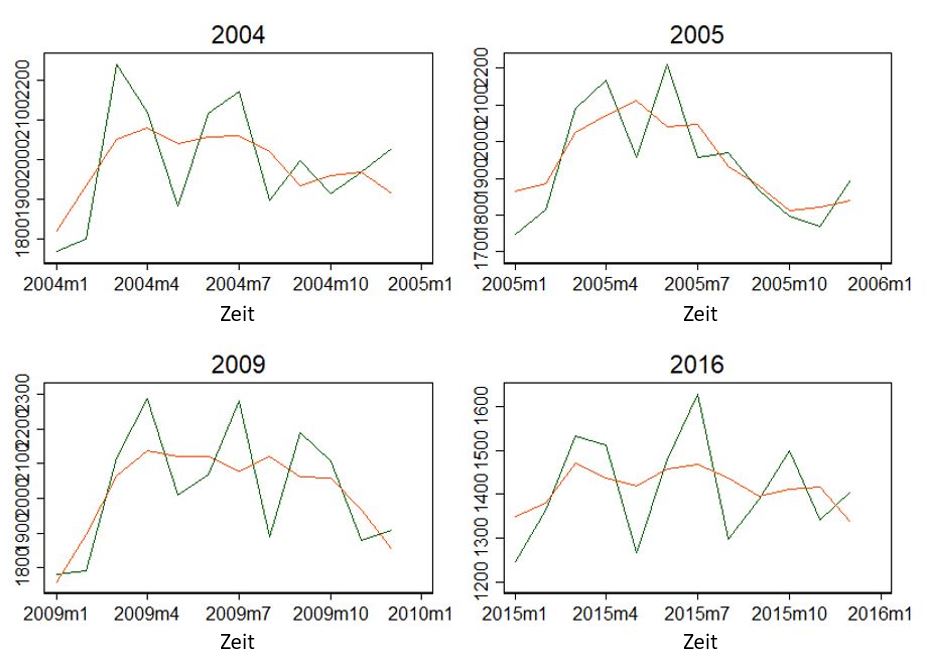
Die Jahre scheinen einen saisonalen Verlauf zu haben. Steigend zum April, dann sinkend, und nochmal steigend zum Juni/Juli? Zumindest sehen die Jahre nicht komplett anders aus.
Zwei Dinge wissen wir nun also: Es scheint einen generellen Trend zu geben – oder vielleicht eher 3? Vor 2008/2009, bis 2011/12 und danach? Und Saisonale-Verläufe – sowohl über das Jahr als auch über die gesamte Zeit.
Die einfachste aller Zeitreihenanalysen: ARIMA
Diese Art der Information lässt sich einfach verarbeiten. Dazu machen wir uns eine simple Zeitreihen-Analyse zu Nutze: die sog. ARIMA-Methode… Autoregressive Integrated Moving Average… Oh man. Nochmal eine recht langweilige Definition und Beschreibung hier.
Wichtiger als zu wissen was ein ARIMA-Model genau tut, ist zu verstehen, wann man es anwendet: nämlich in Situationen, bei denen Mittelwert und Varianz über die Zeit nicht variieren – also stationär sind. Ist das hier der Fall? Der Mittelwert im Jahr 2005 liegt bei 1937.25 und die Standard-Abweichung bei 152.65 Unternehmen. In 2009 hingegen bei 2026.25 und 177.46 Unternehmen.
Ohne großes Testen können wir davon ausgehen, dass die Zeitreihe nicht stationär ist – also eben in Mittel und Varianz über die Zeit durch die Gegend geistert. Eigentlich passt ARIMA also nicht…
Wir können die Daten jedoch ein wenig manipulieren. Also so hinbiegen, dass es aussieht, als wären sie stationär. Stationäre Daten sehen ungefähr aus wie White Noise, also eher so statisches Flimmern. Aber wie machen wir das? Jetzt gehen wir mal so unwissenschaftlich vor, wie es nur geht. Aber eben schnell und vor allem graphisch. Kein großes Rumgerechne nötig.
Datentransformation
Als aller erstes versuchen wir die aller größten Schwankungen herauszubekommen. Dazu könnten wir die Zeitreihe z.B. logarithmieren – denn dann fallen Ausreißer weniger ins Gewicht. Denn eine große Zahlen sind im natürlichen Logarithmus immer noch recht klein. Sieht dann übrigens so aus:
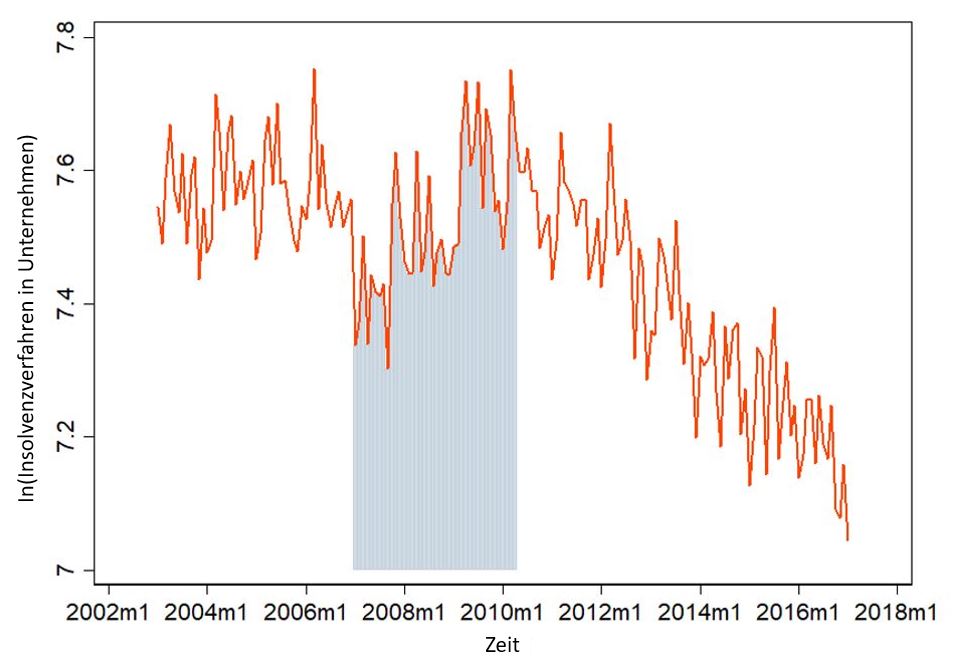
Unser Maximum von 2329 Insolvenzen im Jahr 2006 ist jetzt eben mal auf 7.75 geschrumpft (denn ln(2329) = 7.75). Das sieht schon ein wenig mehr nach white noise aus – aber alles ab ca. 2010 hat noch einen klaren Trend. Es gibt noch mehr Möglichkeiten. Wenn der Logarithmus-Trick nicht ausreicht, kann man ihn noch mit dem First-Order-Difference-Trick koppeln. Das heißt, man bildet die Differenz von Periode zu Periode. Das sieht dann so aus:
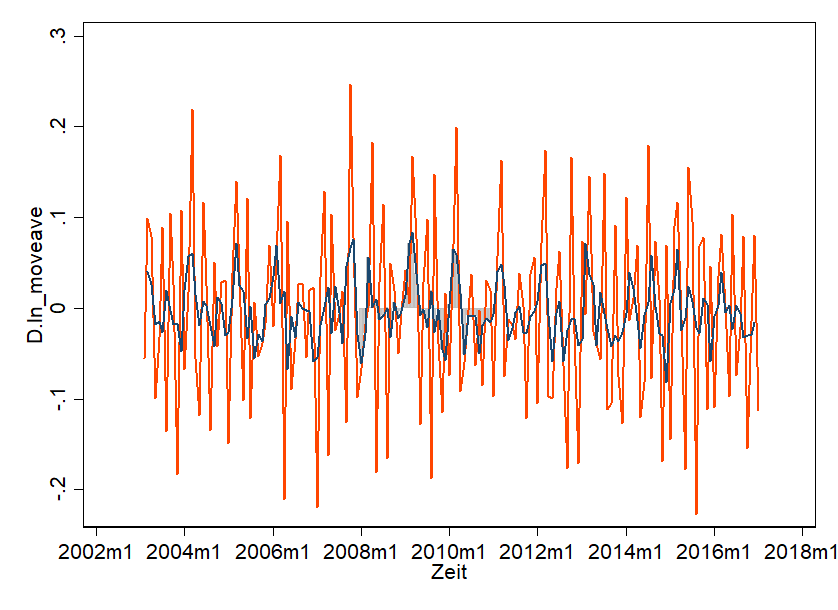
Gezeigt ist der First-Order-Difference und in der Mitte liegend der Durchschnitt. Und das ist ziemlich genau das, was wir suchen! Schön White Noise – also alles sieht super ähnlich aus. Kaum ein Trend ist zu erkennen. Es erscheint willkürlich. Wichtig dabei: wir haben die Daten nicht „kaputt gemacht“ – wir haben sie transformiert und können diese Transformation auch zurückführen.
Der eigentliche Forecast und seine Probleme
Nun können wir uns auch schon an die ARIMA-Methode machen. Dabei müssen wir dem ARIMA-Model noch ein wenig auf die Sprünge helfen. Das „A“ in ARIMA steht für „Autoregressive“. Das bedeutet so viel wie „die eine Periode beeinflusst eine andere“. Und ob das der Fall ist, will ARIMA von uns wissen. Wir können checken, ob das bei uns so ist. Dazu nutzen wir eine ziemlich coole Graphik – i.e. ein Correlogram und das sieht so aus:
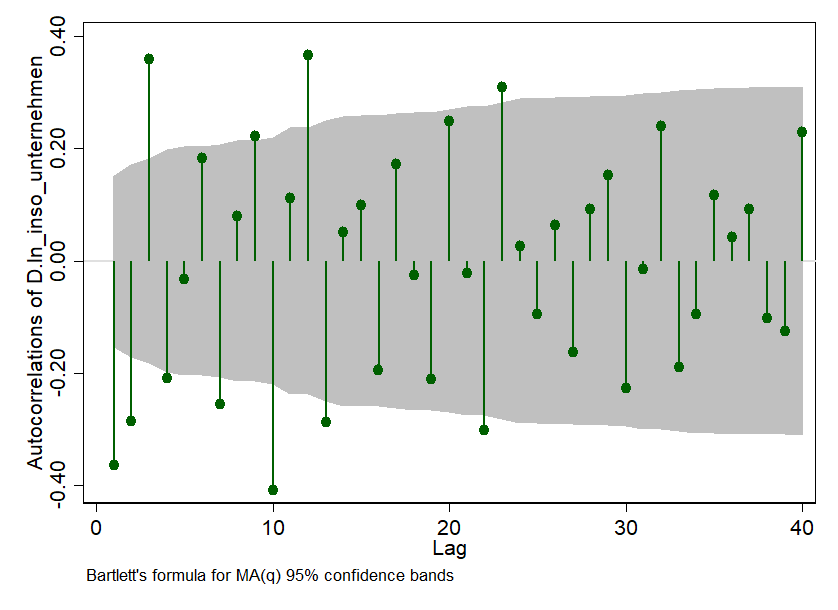
Die kleinen Piekser zeigen uns wie stark die Zeitereihe, die wir observieren, mit sich selbst über die Zeit zusammenhängt. Dazu machen wir uns die Autokorrelation eines Monats zum nächsten zunutze. Die Korrelation zwischen der Anzahl der Insolvenzanträge im letzten verfügbaren Monat und dem zuvor wird bei bei Lag = 1 abgetragen. Bei unserem Beispiel liegt sie bei so ca. -0.38 und ist dazu auch noch signifikant – da der Piekser liegt außerhalb des grauen 95%-Konfidenzintervall. Coole Graphik, was?
Doch was machen wir nun damit: wir sagen unserem ARIMA-Modell, dass zumindest die ersten drei Perioden in Ihrer Korrelation signifikant von Null unterschieden sind und bitten es, das zu berücksichtigen.
Was bringt das Ganze? Wir benötigen diese Information, um ein ARIMA-Modell mit Tools wie Python, R oder Stata zu schätzen. Wir helfen diesen Tools die Abhängigkeiten über die Zeit einzupreisen – und wenn wir das machen, können wir Forecast-Aussagen treffen. Das sieht dann z.B. so aus:
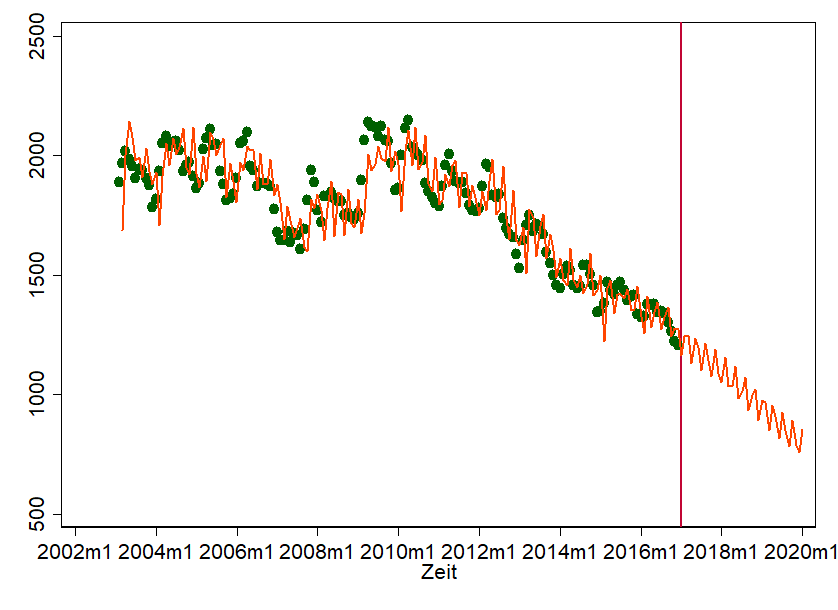
Dies Graph zeigt ein Scatterplot der tatsächlich angefallenen Insolvenzanträge über die Zeit. Das sind die grünen Punkte. Die Linie allerdings ist unser Prediction-Modell. Natürlich ist das alles andere als perfekt. Aber ganz schlecht ist es auch nicht. Einige Punkte treffen wir ganz gut. Wir haben uns zudem die Freiheit genommen, die Vorhersage einfach mal fortzuschreiben. Wir finden, es sieht „halbwegs natürlich“ aus. Das ist zwar noch lange kein Grund, dass Mitte 2018 wirklich weniger als 1000 Insolvenzanträge verzeichnet werden, aber es gibt uns ein grobes Gefühl, wohin die Reise geht.
Wann kann ARIMA eingesetzt werden?
In der simplen Anwendung von ARIMA-Modell liegt auch das Problem – und das wird deutlich, wenn wir mal so tun, als hätten wir selbigen Forecast September 2007 durchgeführt und würden heute unseren Forecast mit der Realität vergleichen:
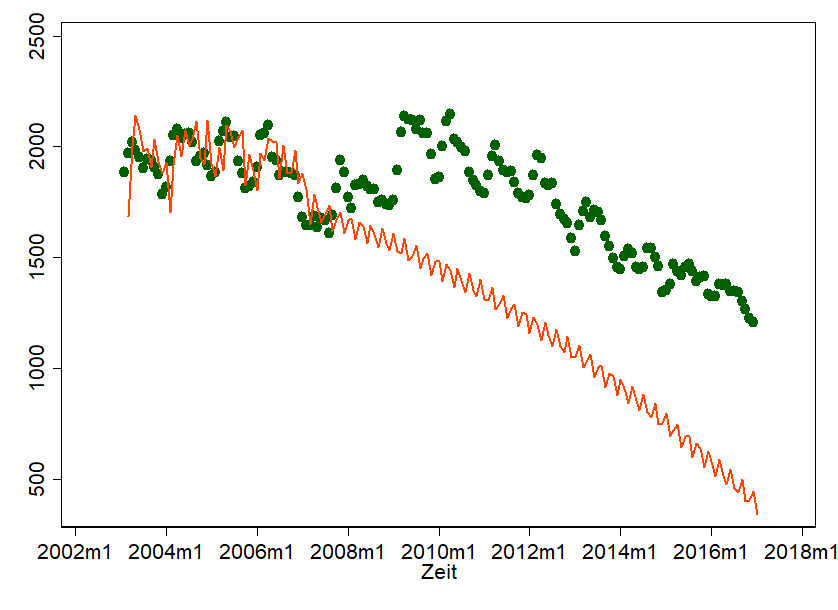
Tja, shit happens. Die Finanzkrise hat uns einen ordentlichen Strich durch die Rechnung gemacht… und so richtig natürlich sieht unser Forecast auch nicht mehr aus. Bei all dem Charme, den ARIMA mit sich bringt, lauert doch die Gefahr, dass wir unterliegende Prozesse komplett aus den Augen verlieren. ARIMA-Forecasts sind daher besonders sinnig, wenn
- die unterliegenden und bestimmenden Beweggründe gut erfasst und erklärt werden können – das ist z.B. oft bei Produktionsdaten so.
- wenn Saisonalität und Trend inhaltlich belegbar sind. Dazu braucht man recht viele Datenpunkte/Perioden – ab 50 geht es meist. Besser ist alles über 100. In den meisten Fällen hingegen sollte man immer zwei bis drei Forecast-Methoden nutzen und sich genau Gedanken machen, warum es zu Unterschieden kommt.
Haben Sie schon eine Idee, wo Sie Zeitreihen in Ihrem Unternehmen untersuchen könnten? Lassen Sie es uns gerne wissen. Wir freuen uns immer über Feedback!

